Butterworth Filter Theorie

Derivation

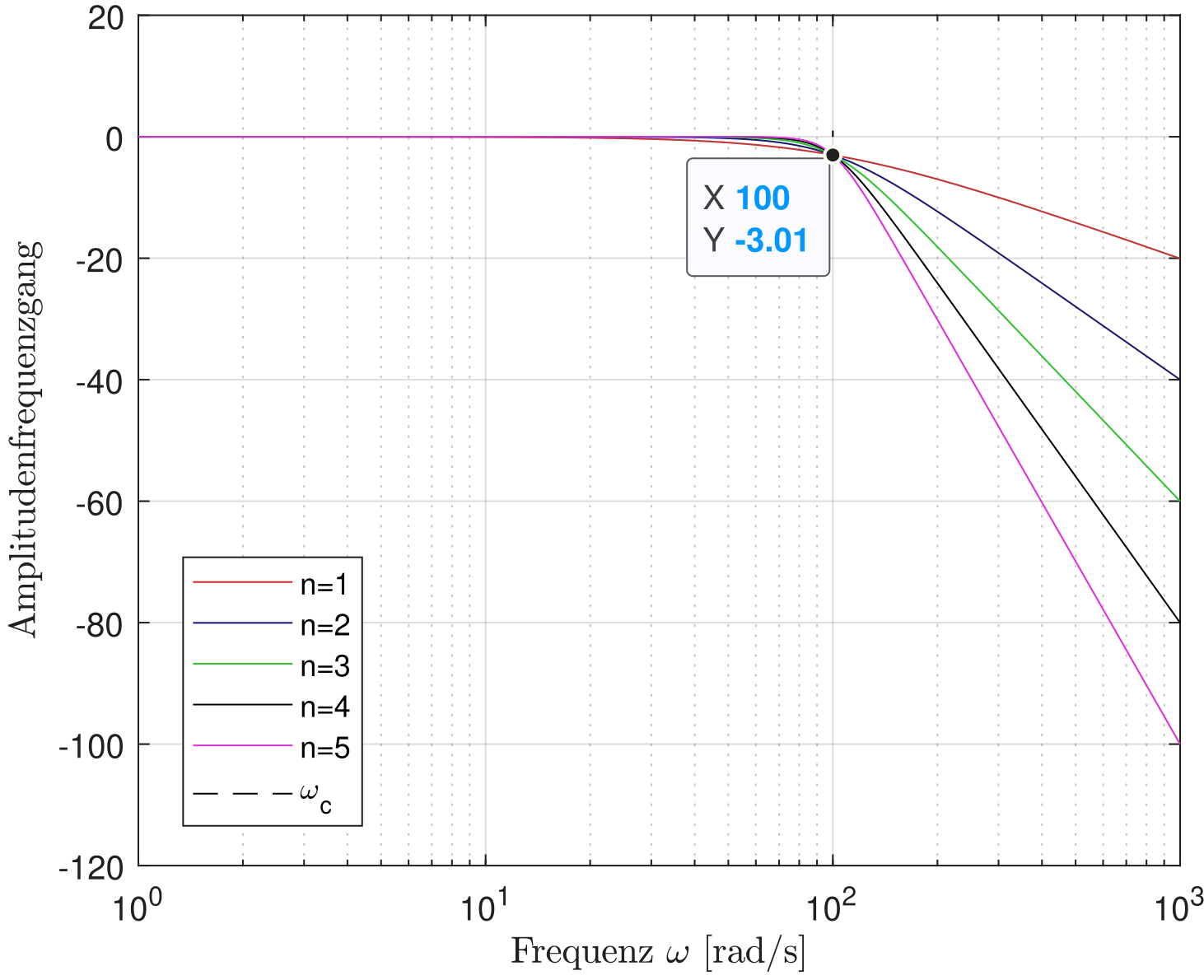
Maßgabe: Amplitudenfrequenzgang soll im Durchlass- und Sperrbereich glatt sein. Dies wird erfüllt durch Polynome der Form \begin{equation} G(\omega) = \frac{G_0}{\sqrt{1+\left(\frac{\omega}{\omega_c}\right)^{2N}}}. \end{equation} Wir definieren den Betrag der Übertragungsfunktion nun als \begin{equation} \left|\underline{H}(j\omega)\right|^2 \overset{!}{=} \frac{G_0}{\sqrt{1+\left(\frac{j\omega}{j\omega_c}\right)^{2N}}}. \end{equation} Wichtige Eigenschaften von Systemfunktionen sind \begin{align} \left|\underline{H}(s)\right|^2 &= \underline{H}(s) \cdot \overline{\underline{H}(s)} \\ \underline{H}(-j\omega) &= \overline{\underline{H}(j\omega)} \end{align} Daraus folgt nun für unsere Systemfunktion $\underline{H}(s)$ \begin{align} \left|\underline{H}(s)\right|^2 = \frac{G_0^2}{1+\left(\frac{s^2}{j^2\omega_c^2}\right)^{N}} = \frac{G_0^2}{1+\left(-\frac{s^2}{\omega_c^2}\right)^{N}}. \end{align} Um das Nennerpolynom aufzustellen bestimmen wir die Nullstellen im Nenner \begin{align} \sqrt[N]{-1} = \left(-1\right)^\frac{1}{N} &= e^{j\pi(2n-1)/N} \\ s_n = p_n = \pm \sqrt{-\omega_c^2e^{j\pi(2n-1)/N}} &= \pm \omega_c^2e^{j\pi(2n+N-1)/(2N)} \end{align} Die daraus resultierenden Polstellen $p_n$ mit $n=1..N$ sind in der $s$-Ebene in einem Kreis mit dem Radius $\omega_c$ und gleichem Winkel zwischeneinander angeordnet.

Normierter Butterworth-Filter 2. Ordnung

Normierung: $\omega_c=1$ rad/s
Die Polstellen befinden sich nun bei \begin{align} p_{1,2,\mathrm{norm}} &= -\frac{1}{\sqrt{2}} \pm \frac{1}{\sqrt{2}}j \\ \underline{H}_{2, \mathrm { norm }}(s) = \frac{1}{\left(s-p_1\right)\left(s-p_2\right)} &\stackrel{s \rightarrow \frac{s}{\omega_c}}{\Longrightarrow} \underline{H}_2(s)=\frac{1}{\left(\frac{s}{\omega_c}-p_1\right)\left(\frac{s}{\omega_c}-p_2\right)} \\ \underline{H}_2(s)=\frac{\omega_c^2}{s^2-\omega_c s(p_1+p_2)+\omega_c^2 p_1 p_2} &= \frac{\omega_c^2}{s^2+\sqrt{2} \omega_c s+\omega_c^2} \\ p_{1,2} &= \omega_c \cdot p_{1,2, \mathrm { norm }} \end{align}